Time Series Analysis
Large pre-trained models have dominated numerous areas. Fundamentally speaking, they effectively compress all available information to achieve such remarkable performances. However, when the time dimension is added, it becomes extremely difficult, if not impossible, to be able to compress all the information. Therefore, time series analysis is one of the few areas that are not dominated by large pre-trained models. At the same time, it has a wide range of applications such as finance, weather forecasting, and industrial process control.
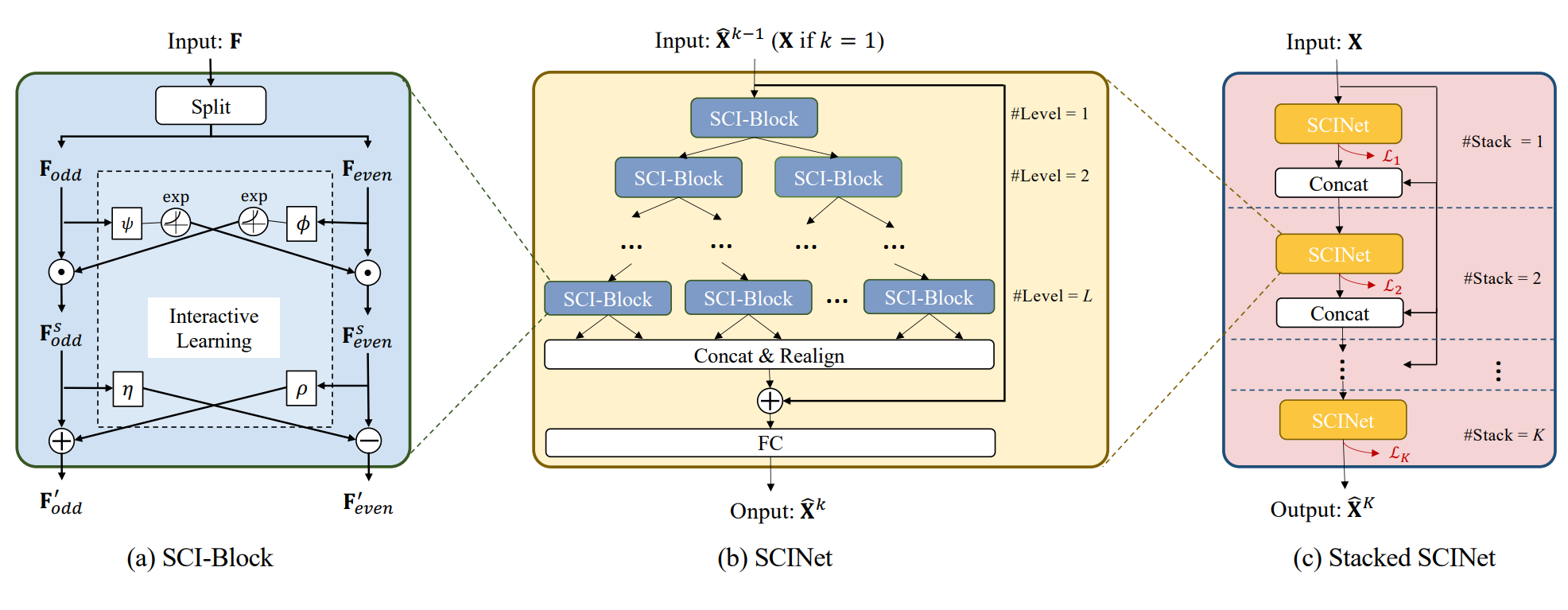
Conventional approaches treat time series as sequential data and employ Transformer models to tackle these tasks. However, we posit that Transformers may not be the most suitable choice for time series tasks due to several reasons. Firstly, the attention mechanism in Transformers solely discerns the correlation among tokens, falling short in extracting the temporal relationships inherent in time series data. Secondly, Transformers depend on positional embeddings to portray relative positional information, which fails to adequately capture the temporal essence of the data. Lastly, the tokenization of time series data often lacks meaning since it generally comprises multiple data points from various channels at a single point in time.
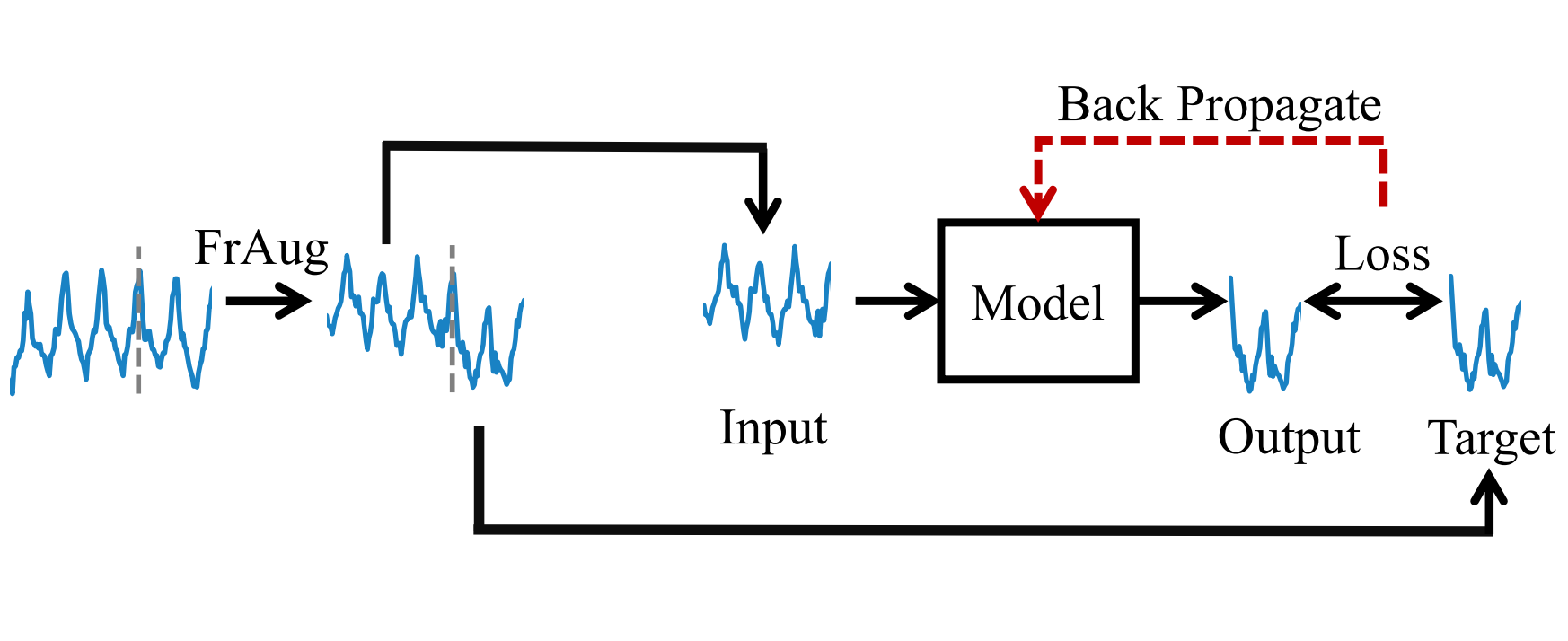
In light of these constraints, we seek to challenge the prevailing use of transformer-based models for time series analysis. We have pioneered a novel model called DLinear, which utilizes a straightforward linear combination in the temporal domain. Remarkably, DLinear consistently outperforms other transformer-based methods in time series forecasting tasks. Moreover, we have transitioned our attention to the frequency domain, interpreting time series as samples of signals originating from real-world physical systems. To amplify the performance of time series forecasting models, we have crafted FrAug, a frequency domain augmentation method specifically designed for this purpose. FrAug effectively enhances the predictive prowess of time series forecasting models.
Looking ahead, our research team intends to delve deeper into a variety of time series analysis problems, including probabilistic forecasting and viewing forecasting as a generative task. We are also eager to explore the application of our findings across diverse domains, paving the way for progress in sectors such as finance, climate science, and healthcare.